Standardize a dataset. When and why?

Posted bylearndataaPosted inCoding Tutorial

Standardization is done to bring features of vastly different magnitudes into a similar range.

In this post you will learn:

  1. When to standardize a data set for machine learning?
  2. How to use Scikit-learn’s preprocessing tools:
    • .scale()
    • .StandardScaler()

Introduction

“Standardization of datasets is a common requirement for many machine learning estimators implemented in scikit-learn.”

– Scikit-learn

Distance based machine learning estimators calculate distances based on values for features. Ideally these values should be in a similar range of magnitude for correct predictions. However, in a dataset if the values of a feature are say 100000 times that of another feature then the calculated distances would be of a higher magnitude as well. This may cause the estimator to give more importance to the feature of higher magnitude. Thus, it could lead to incorrect predictions. Standardization comes to rescue! It helps to bring features of different magnitudes into a similar magnitude range. This is shown in the plot below for K-Means clustering with and without standardization:

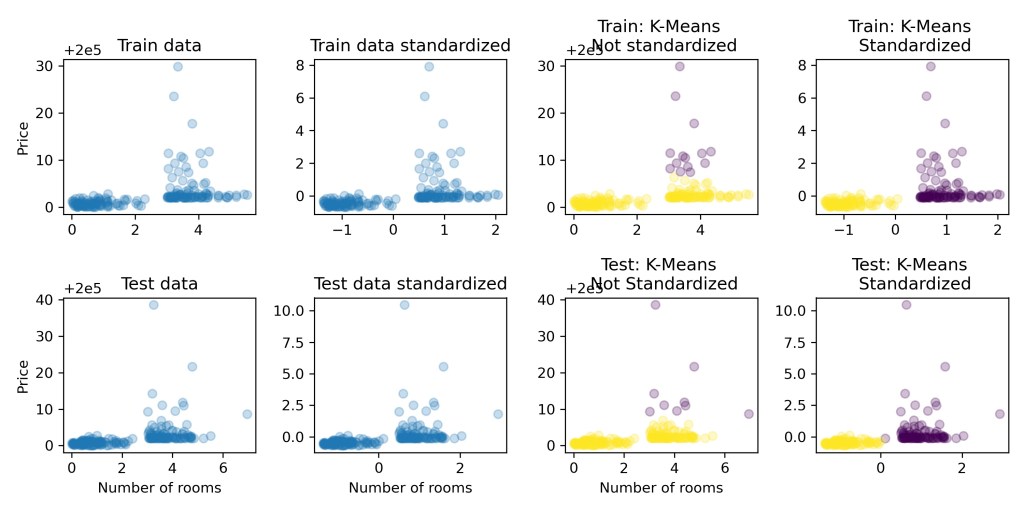
K-means clustering on a housing data set with and without standardization. Note the changes in x and y axis after standardization. The plots in the 3rd column show incorrectly identifies two clusters as the same (‘yellow’ color) without standardization. The plots in the last (4th) column on the right show correctly identified clusters (‘yellow’ and ‘violet’ colors) after standardization. (Note: The code for above plots not discussed in this post.)

When to standardize a data set?

Usually standardization is done on a train data set. The .StandardScaler() calculates the mean and variance for the train data. This can then be used to transform the train, validation and test data sets.

How to standardize a data set?

Scikit-learn’s preprocessing library provides .scale() and .StandardScaler(). The calculations are in two steps:

  • mean removal: subtract mean of a feature from its individual values
  • variance scaling: divide each value of a feature by its standard deviation (i.e. square root of variance)

Equation 1:

Using .scale():

This is an easiest way to standardize data by directly applying the .scale() method.

# Import libraries
import numpy as np
from sklearn import preprocessing

# Data
x = np.array([[100000, 150000, 350000, 200000],
             [1,2,3,2]])
x = x.T # convert rows to columns
print("Before standardization:\n", x, '\n')

# Using .scale()
x_standardized = preprocessing.scale(x)
print("After standardized using .scale():\n", x_standardized, '\n')

# Standardizing manually:
x_std_manual = (x - np.mean(x, axis=0))/np.std(x, axis=0)
print("After standardized manually:\n", x_std_manual)

Before standardization:
 [[100000      1]
 [150000      2]
 [350000      3]
 [200000      2]] 

After standardized using .scale():
 [[-1.06904497 -1.41421356]
 [-0.53452248  0.        ]
 [ 1.60356745  1.41421356]
 [ 0.          0.        ]] 

After standardized manually:
 [[-1.06904497 -1.41421356]
 [-0.53452248  0.        ]
 [ 1.60356745  1.41421356]
 [ 0.          0.        ]]

Using .StandardScaler():

The .StandardScaler.fit() method is first applied to the train data to calculate the mean and variance. These value are then used by the .transform() when it is applied to the train and test data to standardize. The implementation is shown below:

Step- 1

Create a sample data set for train and test using Numpy array as below:

# Import libraries
import numpy as np
from sklearn import preprocessing

# Data: Train
X_train = np.array([[100000, 150000, 350000, 200000], # Price of house
             [1,2,3,2]]) # Number of rooms in house
X_train = X_train.T # convert rows to columns
print("Before standardization, X_train:\n", X_train, '\n')


# Data: Test
X_test = np.array([[110000, 130000, 250000, 290000], # Price of house
             [2,1,3,3]]) # Number of rooms in house
X_test = X_test.T
print("Before standardization, X_test:\n", X_train, '\n')

Before standardization, X_train:
 [[100000      1]
 [150000      2]
 [350000      3]
 [200000      2]] 

Before standardization, X_test:
 [[100000      1]
 [150000      2]
 [350000      3]
 [200000      2]]

Step-2

Use the .fit() method to calculate the mean and variance for the X_train data.

scaler = preprocessing.StandardScaler().fit(X_train)
print('X_train mean:\n', scaler.mean_, '\n')
print('X_train variance:\n', scaler.var_)

X_train mean:
 [2.e+05 2.e+00] 

X_train variance:
 [8.75e+09 5.00e-01]

Step-3

Use the .transform() method to apply the .fit() from Step-2 to the X_train data.

X_train_standardized = scaler.transform(X_train)
print("X_train_standardized:\n", X_train_standardized, '\n')
print('Mean of X_train_standardized:\n',np.mean(X_train_standardized), '\n')
print('Variance of X_train_standardized:\n',np.var(X_train_standardized))

X_train_standardized:
 [[-1.06904497 -1.41421356]
 [-0.53452248  0.        ]
 [ 1.60356745  1.41421356]
 [ 0.          0.        ]] 

Mean of X_train_standardized:
 0.0 

Variance of X_train_standardized:
 0.9999999999999999

In the above output note that the mean of X_train_standardized is zero (mean removal) and the variance is 0.99 ie. ~1 (unit variance).

Step-4

Apply .transform() to the X_test data

X_test_standardized = scaler.transform(X_test)
print("X_test_standardized:\n", X_test_standardized, '\n')
print('Mean of X_test_standardized:\n',np.mean(X_test_standardized), '\n')
print('Variance of X_test_standardized:\n',np.var(X_test_standardized))

X_test_standardized:
 [[-0.96214047  0.        ]
 [-0.74833148 -1.41421356]
 [ 0.53452248  1.41421356]
 [ 0.96214047  1.41421356]] 

Mean of X_test_standardized:
 0.1500505711053944 

Variance of X_test_standardized:
 1.064627683253802

In the above output note that the mean of X_test_standardized is close zero (mean removal) and the variance is close to 1 (unit variance). The values are slightly off because remember that here the .transform() used the mean and variance for X_train and not X_test.

2 thoughts on “Standardize a dataset. When and why?”

  1. Hello

    If I want to standardize my data for a regression model with cross-validation…

    There are three alternatives:
    – standardize the training data and apply this standardization to the testing (or validation) data.
    – standardize the training data and the testing data separately.
    – standardize all the data together.

    What is the difference?
    What is the best method?

    Like

    Reply

    1. Great question! The three alternatives you’ve mentioned each have their considerations.

      – (recommended) Standardizing the training data and applying it to the testing (or validation) data ensures consistency and avoids data leakage.

      – Standardizing the training and testing data separately allows each set to have its own scaling parameters, which might be important if they come from different distributions. This also means that the training data is not representative of the overall population. The resulting model may not be able to generalize well on the unseen dataset.

      – Standardizing all the data together considers the entire dataset, but be cautious with this approach as information from the testing set might influence the training set. The resulting model may not be able to generalize well on the unseen dataset.

      The best method depends on your specific dataset and the characteristics of your problem. Generally, option 1 is a safe default, but it may/may not help experimenting to see which approach works best for your regression model with cross-validation.

      Hope this helps! If you have more questions, feel free to ask.

      Like

      Reply

Leave a comment